TSNE embedding of the swiss roll dataset

We show how to compute a TSNE embedding with TorchDR on the swiss roll dataset.

# Author: Rémi Flamary <remi.flamary@polytechnique.edu>
#         Hugues Van Assel <vanasselhugues@gmail.com>
#
# License: BSD 3-Clause License

import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll

from torchdr import TSNE

Load toy images

First, let’s load swiss roll dataset from sklearn.

n_samples = 500

X, t = make_swiss_roll(n_samples=n_samples, noise=0.1, random_state=0)

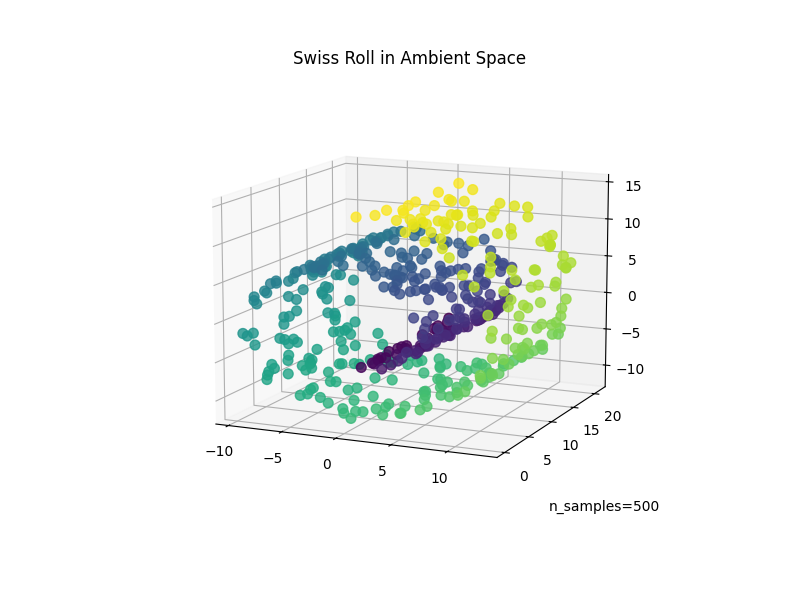
Plot the dataset

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, s=50, alpha=0.8)
ax.set_title("Swiss Roll in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s=f"n_samples={n_samples}", transform=ax.transAxes)

Compute the TSNE embedding

tsne = TSNE(n_components=2, perplexity=10, max_iter=200)

X_embedded = tsne.fit_transform(X)

Plot the TSNE embedding

plt.figure(figsize=(8, 6))
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=t, s=50, alpha=0.8)
plt.title("TSNE embedding of the Swiss Roll dataset")

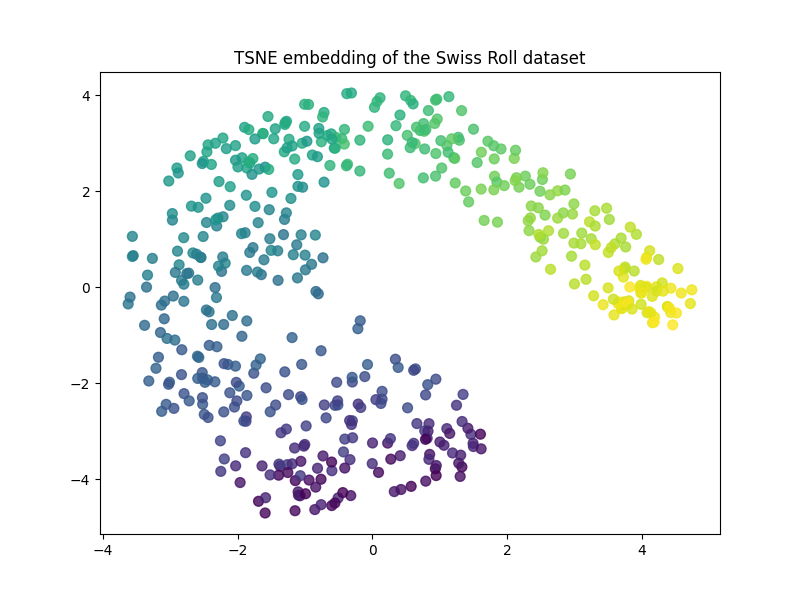
Text(0.5, 1.0, 'TSNE embedding of the Swiss Roll dataset')

See the impact of perplexity

perplexity_values = [2, 5, 10, 20]
X_embedded = []
for perplexity in perplexity_values:
    if len(X_embedded) == 0:
        init = "pca"
    else:
        init = X_embedded[-1]
    tsne = TSNE(n_components=2, perplexity=perplexity, max_iter=200, init=init)
    X_embedded.append(tsne.fit_transform(X))

plt.figure(figsize=(12, 4))

for i, perplexity in enumerate(perplexity_values):
    plt.subplot(1, 4, i + 1)
    plt.scatter(X_embedded[i][:, 0], X_embedded[i][:, 1], c=t, s=50, alpha=0.8)
    plt.title(f"Perplexity = {perplexity}")

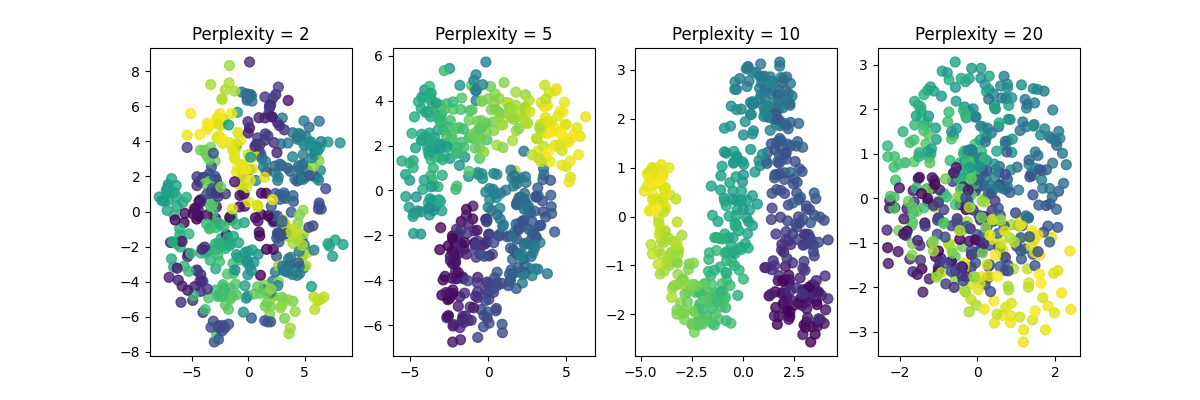
We can observe that the perplexity parameter significantly influences the embedding. When the perplexity is too low, the embedding captures only short-range dependencies and fails to capture the manifold’s geometry. Conversely, when the perplexity is too high, points that are distant on the manifold but close in the ambient space are mistakenly considered neighbors.